A Merkle tree is specified in section 7 of the Bitcoin White Paper and explained in more detail on Dr Wright’s blog on Merkle trees.

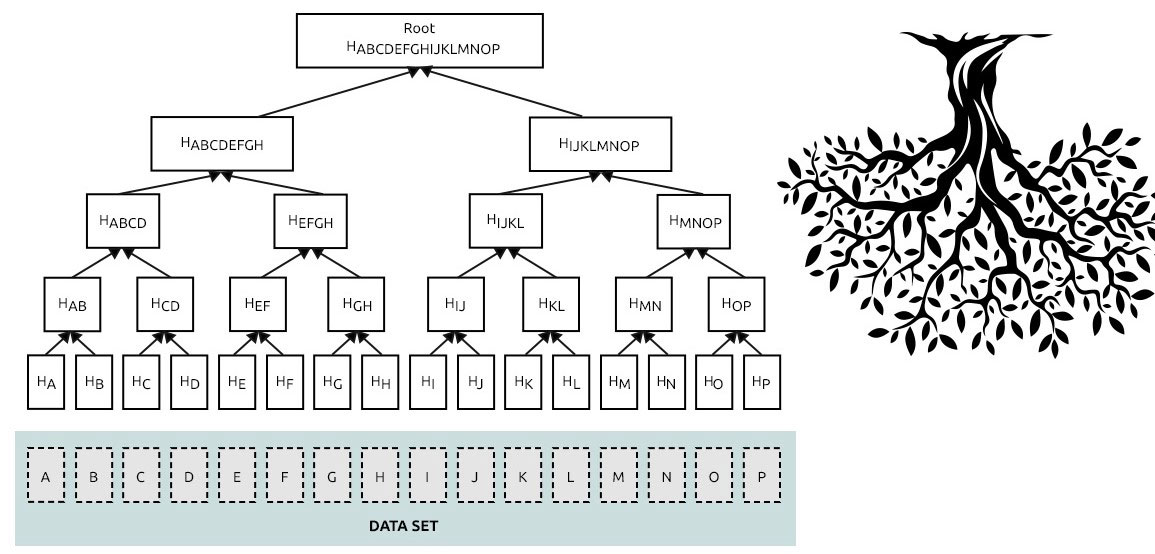
Merkle trees are hierarchical data structures that enable secure verification of collections of data. It is a tree structure with branches and leaves. Both contain hashes.

Each leaf contains a unique hash of a block on the chain. The nodes of each branch of the tree contain a hash of every child (leaf) in that branch. The leaf nodes of the tree contain hashes of data, while the branch nodes are comprised of hashes of their child nodes concatenated together leading back to the root of the tree.

The root of the tree contains a hash denoting every branch of that tree. Therefore, the tree’s root has information about everything in its structure.

Merkle trees are a type of a tree from the binary tree family. They have similarities to other types of trees from the binary tree family, and it is important to understand the differences and similarities between them.

A Binary tree is a tree where each node in the tree has at most two children. In a normal binary search tree, the placement of nodes depends almost entirely on the order in which they were added.

A B-tree is a self-balancing tree structure that allows for nodes with more than two children. Each internal node of the B-tree contains several key-value pairs which divide the subtrees in the node. Internal nodes can contain both keys and child nodes. The number of child nodes of a node will be one more than the number of keys stored. The keys are stored in internal nodes but not in the records contained in the leaves.

A B+ tree is a tree structure that can contain many children per node. Each internal node of the B+ tree contains a pointer to another node in the tree, or if the node is a leaf node, a pointer to data. This essentially makes the internal nodes of the tree a multi-level index to the data pointed to by the leaf nodes of the tree. This ‘fan out’ arrangement significantly reduces the computational effort to find information across the tree.

The difference between a B+ tree and a Merkle tree is that a Merkle Tree is entirely constructed of hashes. In other words, a Merkle Tree is a Hash Tree and it’s used for a different purpose. Rather than searching a Merkle Tree for the location of data like a B+ tree, a Merkle Tree stores a hash or fingerprint of data and links it via concatenated hashes to the root hash of the tree.

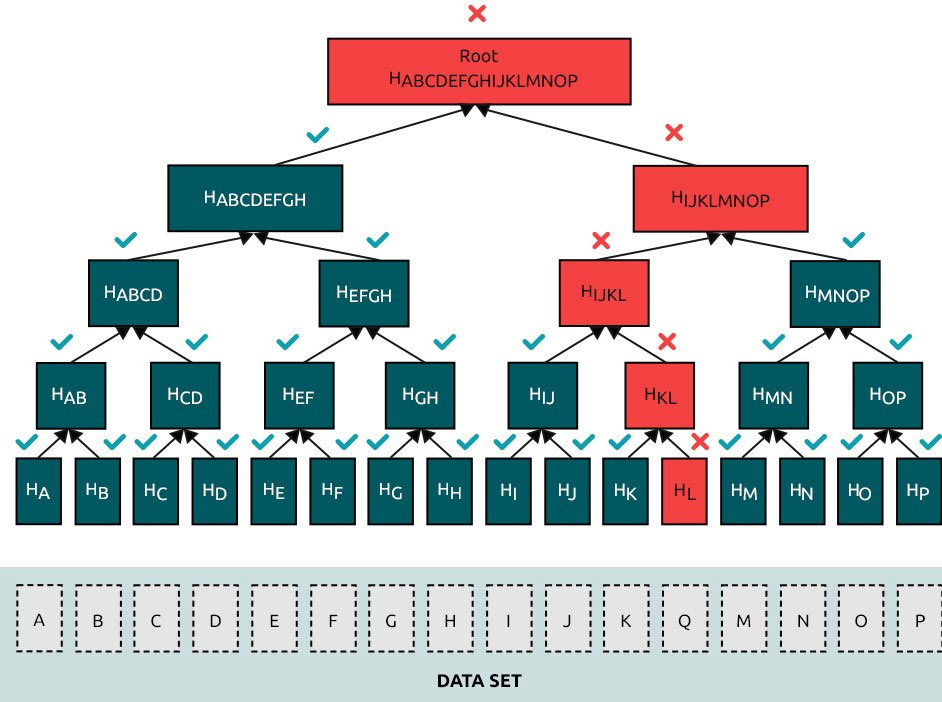
Each level of the tree, starting from the leaf nodes at the bottom, is comprised of the hash of the two child node hashes concatenated together. If you have the pair value for each level of the tree from a leaf node to the root (the 1-pair hash needed for each level is known as the Merkle path), it is possible to recalculate the root value of the tree by using a series of simple hashes – a Merkle proof.

In Bitcoin, the root value of the Merkle tree is stored in the Block Header in each block. Block headers represent blocks of transactions by including the Merkle root of a Merkle tree of transactions that were time-stamped in the block.

If you have the block header (which is only 80 bytes in size) and the Merkle paths of your transactions, you can recalculate the Merkle root of the tree your transaction is in. You can then compare this calculation to make sure it matches the Merkle root – to calculate the Merkle proof. At a basic level – this is how SPV (Simplified Payment Verification) works – as described in Section 8 of the Bitcoin white paper.

As per Dr Wright’s post on Merkle trees and SPV, to verify that a given transaction has been processed and included in a block, SPV checks perform the Merkle proof for each input of the transaction to confirm the inputs exist and were mined.

SPV is required for massively scaling the number of transactions BitcoinSV can process. Large block sizes and Merkle trees are needed to massively scale the number of transactions in a block.

If a blockchain is not aimed at scaling, using Merkle trees is a poor design decision because they are less secure than simply storing transaction IDs (the double sha256 hash of a serialised transaction is known as the TXID).

Dr Wright wrote a useful blog post explaining the double hash requirement. The post focuses on how the double hash is used to calculate the TXID, however, the same logic applies to Merkle proofs.

Cryptographic hash functions produce hashes with a defined output length — in the case of sha256, the output length is 256 bits. Therefore, when you calculate a hash from any length input, you maintain the collision resistance of the hash function because the set of possible inputs is very large.

However, when you use a fixed length input like a hash, you lose roughly 1 bit of collision resistance because the set of possible inputs is reduced. For example, for each hash of a sha256 message digest, collision resistance would be reduced from 2^256 to 2^255, 2^255 to 2^254, 2^254 to 2^253 and so on.

By having to perform a series of hashes like a Merkle proof, you lose collision resistance. Therefore, the trade-off with using a Merkle tree is supporting massive scalability for a slight security hit. However, Bitcoin is secured via economic incentives, not cryptographic hash functions. By using a new key-pair for each new address or locking script solution in a transaction output, and ensuring each transaction output utilises the advantage of the extremely low transaction fee of BSV by ensuring each output contains a small amount of BSV, the cost to find a collision far outweighs the resulting reward in finding one.

Merkle trees operate more efficiently at scale. According to ZeMing M. Gao:

The efficiency of a Merkle tree increases exponentially with the size of the data set. For example, take the BTC block, which has less than 5000 transactions per block. Under Merkle tree’s hashing scheme, which combines every two data entries into one hash, and then every two hashes into another combined hash, and so on, 5000 transactions would need 12 levels of hashing. In comparison, a block that has 1 billion transactions would only need 30 levels of hashing. Although the total number of transactions increased 200,000 times, hashing levels increase less than three times (30 versus 12).

In the case of BTC, the risk can be almost eliminated by switching the data structure for calculating the root hash of a block from a Merkle tree to that of a simple array. That way, instead of having to calculate a series of hashes like is needed in a Merkle proof, a single hash can be calculated using the full array of TXIDs.

BTC has no need to use a Merkle tree. Unless there is an unbounded block size that continues to increase in size, there is no requirement to use a Merkle tree. With BTC’s limited block sizes the Merkle root in the block header could simply be replaced with a hash of the list of transactions because this mechanism contradicts SPV as defined in section 8 of the Bitcoin white paper, is not future-proofed, and therefore will never scale.